Math run around? (Simple algebra question.)

[MK3Brent]

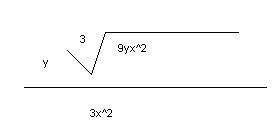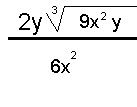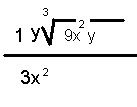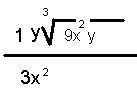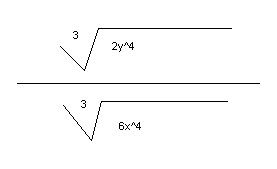
I saw this problem a while ago... and never having problems before with this sort of thing, I gave it a shot.

It's driving me nuts!

(Rationalize the denominator.)

Since we know the index is "3" I'm looking for cubes factors of "6":

Normally when finding squares... it's really easy, you can just multiply by itself.

so: 6*6=36

the cube root of 6x^4 multiplied by the cube root 36x^4 = the cube root of 216x^8

Now multiply the numerator by the cube root 36x^4 and you get: the cube root of 72x^4y^4

This successfully gives you a cubed root in the denominator, 6...

but then I get lost some.


Anyone remember this stuff?

Here's the answer:

 

[MK3Brent]

n/m I got it.

cube root of 72x^2y^4 is 8*9y^4x^2

and the cube root of 216x^6 is 6x^2

Now reduce:

 

[greg88]

FTW!!1!1!!!!1

 

[7M-GTE]

EDIT:... never mind... after a closer look you already have the answer and I didn't figure it out...

 

[MK3Brent]

EDIT:... never mind... after a closer look you already have the answer and I didn't figure it out...

Yeah, my problem was trying to make a cube out of the exponents.

Thanks for reading though!

 

[7M-GTE]

^^^ I was gonna say just take the reciprocal of the denominator to get rid of it... but it shows that you have a denominator in the final answer...

 

[MK3Brent]

You can't do that if you're rationalizing.

if you were given a "9" in the denominator... that's "3*3" to make it a cube you multiply of course by one more "3"


With this problem I have one "6" so I need 2 more... "6*6" = 36.

The exponent power was where I was confused... I thought the only next available CUBE was 8.... but with exponents you don't need to have a cube, rather an evenly divisible power w/ respect to the index.

So with 36x^2 multiplied by the original denominator, you'll get something that will totally get rid of the original radical.